
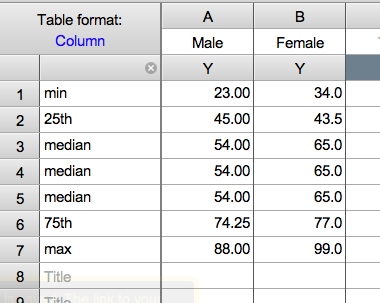
The estimated probability of surviving through both Year 1 and Year 2 is therefore (95/100)x(82/92)=0.8467. And if one does survive through Year 1, the conditional probability of then surviving through Year 2 is 82/92=0.8913. The estimate for surviving through Year 1 is simply 95/100=0.95. Kaplan-Meier Survival Probability Estimate And so on for the other years shown.Īs illustrated in the next table, the Kaplan-Meier procedure then calculates the survival probability estimate for each of the t time periods, except the first, as a compound conditional probability. So the number surviving Year 2 is 92-10=82 and the number at risk at the beginning of Year 3 is 92-3-10=79. Another 3 subjects become unavailable during the second year and another 10 die. The number surviving the first year is therefore 100-5=95 and the number at risk at the beginning of Year 2 is 100-3-5=92. Of the 100 subjects who are at risk at the beginning of the study, 3 become unavailable during the first year and 5 die. The adjacent table shows how these conventions would work out for the present example.

In this way the fudging is kept conceptual, systematic, and automatic. May be paraphrased by saying that deaths recorded as of t are treated as if they occurred slightly before t, and losses recorded as of t are treated as occurring slightly after t. Kaplan and Meier, recognizing that any attempt to salvage this information would involve a certain amount of "fudging," proposed that subjects who become unavailable during a given time period be counted among those who survive through the end of that period, but then deleted from the number who are at risk for the next time period. Yet, if we were simply to omit them from the study, we would be losing valuable information: namely, that the 3 subjects who became unavailable during Year 2 survived at least through Year 1 that the 3 who became unavailable during Year 3 survived at least through Year 2 and so on. The question in a situation of this sort is: What shall we make of the subjects who become unavailable in a given time period? (Within the context of the Kaplan-Meier procedure, the subjects who become unavailable are spoken of as censored.) We in fact do not know whether these subjects survived or died. In real-life research the loss rate would of course not normally be so uniform as this. For the sake of numerical simplicity I am showing 3 subjects becoming unavailable in each of the five years. Another 3 become unavailable during the second year and another 10 are known to have died by the end of the second year.

Of the 100 subjects who are "at risk" at the beginning of the study, 3 become unavailable during the first year and 5 are known to have died by the end of the first year. To illustrate the complication in this sort of situation, consider the following hypothetical scenario. Typically there are subjects lost along the way for reasons unrelated to the focus of the study. The survival of 87 subjects at the end of the first year would give a one-year survival probability estimate of 87/100=0.87 the survival of 76 subjects at the end of the second year would yield a two-year estimate of 76/100=0.76 and so forth.īut in real-life longitudinal research it rarely works out this neatly. If all the subjects remained accessible throughout the entire length of the study, the estimation of year-by-year survival probabilities for subjects of this type in general would be an easy matter. Suppose that 100 subjects of a certain type were tracked over a period of time to determine how many survived for one year, two years, three years, and so forth.


 0 kommentar(er)
0 kommentar(er)
